Definizione assiomatica di probabilità #
Assiomi di Kolmogorov #
Dato un esperimento che preveda più esiti possibili e a cui è associato uno spazio campione \(S\), e dato un evento \(E \subset S\), si definisce probabilità di \(E\) come:
\[ P(E) \in \mathbb{R} \]
Assioma 1 #
\[ 0 \leq P(E) \leq 1 \]
Assioma 2 #
\[ P(S) = 1 \]
Assioma 3 #
Siano \(E_1, E_2, \dots \subset S \) mutuamente esclusivi (o disgiunti), allora vale:
\[ P\left(\bigcup_{i=1}^{m} E_i\right) = \sum_{i=1}^{m} P(E_i) \]
Ovvero, la probabilitù dell’unione degli eventi è uguale alla somma delle probabilità dei singoli eventi.
Conseguenze #
Proprietà 1 - Complementare #
Dato un evento \(E \subset S\), vale:
\[ P(E^C) = 1 - P(E) \]
dove con \(E^C\) si intende il complementare di \(E\).
Dimostrazione #
\(E \cup E^C = S \\ E \cap E^C = \emptyset \\ \underbrace{1 = P(S)}_{\text{Assioma 2}} = \underbrace{P(E \cup E^C) = P(E) + P(E^C)}_{\text{Assioma 3}}\\ P(E) + P(E^C) = 1 \rightarrow P(E^C) = 1 - P(E) \quad \blacksquare\)Proprietà 1bis - Insieme vuoto #
\[ P(\emptyset) = 0 \]
Dimostrazione #
\(S^C = \emptyset \\ P(\emptyset) \underbrace{=}_{\text{P1}} P(S^C) = 1 - P(S) \underbrace{=}_{A2} 1-1 = 0 \quad \blacksquare\)Proprietà 2 - Proprietà di un sottoinsieme #
Siano \(A, B \subset S \quad \text{con} \quad A \subset B\), si dimostra che:
\[ P(A) \leq P(B) \]
Attenzione al minore uguale.
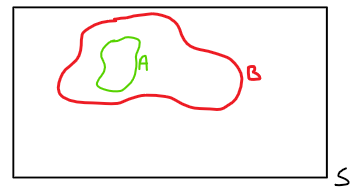
Dimostrazione #
\( B = A \cup (B \cap A^C) = A \cup (B\setminus A) \)
Per costruzione \(A \cap (B \setminus A) = \emptyset \). Quindi \(A\) e \((A\setminus B)\) sono mutuamente esclusivi.
\( P(B) = P(A \cup (B \setminus A)) = P(A) + P(B \setminus A) \)
Per l’assioma 1, \(P(B\setminus A) \ge 0\), quindi
\( P(B) = P(A) + P(B \setminus A) \ge P(A) \rightarrow P(B) \ge P(A) \quad \blacksquare \)